(Plausible) Random Geography Generation with PostGIS: Fluviation
Welcome to Squaria.
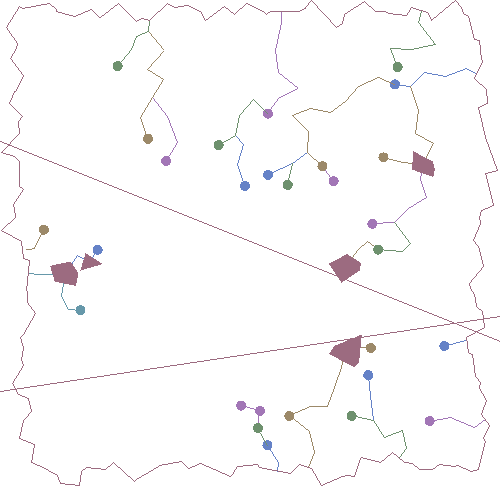
Squaria is a continent of highly unstable geography defined by a single SQL query (with, as we'll see, many, many CTEs). Its only consistent properties at the moment are its boxy shape and the two unnervingly straight mountain ranges that cross its breadth and meet on its lower eastern edge. Those mountains are impossible, but today's topic is fluviation, that is, rivers and riverine lakes; we'll see about plausible plate tectonics some other time, maybe.
The ever-shifting border of Squaria is defined by a Voronoi diagram within a 100-unit envelope, similar to Paul Ramsey's random polygon generation. Other shapes are of course easily achievable, and I'm probably going to steal his circular envelope outright in the future, but squares are easy to demo.
with recursive envelope as (
select st_makeenvelope(0, 0, 100, 100) as geom
), voronoi_unclipped as (
select (st_dump(st_voronoipolygons(
g1 => st_generatepoints(
envelope.geom,
500 -- increase this for a finer polygon mesh
),
tolerance => 0.0,
extend_to => envelope.geom
))).geom as poly
from envelope
), voronoi as (
-- clip the Voronoi diagram to only those polys fully inside the envelope
select voronoi_unclipped.poly
from envelope
join voronoi_unclipped on st_contains(envelope.geom, voronoi_unclipped.poly)
), border as (
select st_boundary(st_concavehull(st_union(poly), 0)) as linestr
from voronoi
)
select * from border;
But it's not just the border that we're concerned about here. If you want to simulate fluviation, you have to go at least a little distance toward simulating fluid mechanics. Water famously flows downhill; a downhill implies an uphill implies height. Let's add those mountain ranges and generate a heightmap while trying not to think too hard about the fact that PostGIS supports a third dimension, making full-scale volumetric simulation theoretically achievable.
All these CTEs build on each other, so if you're following along for fun, you'll need to combine the statements (minus the final selects in each, which just output the current step). I'll post the whole thing at the end too.
with mountain_range as (
with nonrandom_line as (
select st_makeline(st_point(0, v.y1), st_point(100, v.y2)) as linestr
from (values (70, 30), (20, 35)) as v (y1, y2)
)
select
st_collect(voronoi.poly) as geom,
st_collect(nonrandom_line.linestr) as linestr
from voronoi
cross join nonrandom_line
where st_intersects(voronoi.poly, nonrandom_line.linestr)
), heightmap as (
select
voronoi.poly,
-- height is a function of distance from the mountains, also factoring in
-- x-position (Squaria's east is lower than its west) and a little random
-- variance to make things interesting
100
- (min(st_distance(voronoi.poly, mountain_range.geom)) * 1.5)
- (st_x(st_centroid(voronoi.poly)) * 1.5 / 10)
+ (random() * 6 - 3)
as height
from voronoi
cross join mountain_range
group by voronoi.poly
)
select
st_collect(
st_translate(
st_scale(st_letters(round(h.height)::text), .03, .03),
st_x(st_centroid(h.poly)),
st_y(st_centroid(h.poly))
)
)
from heightmap as h;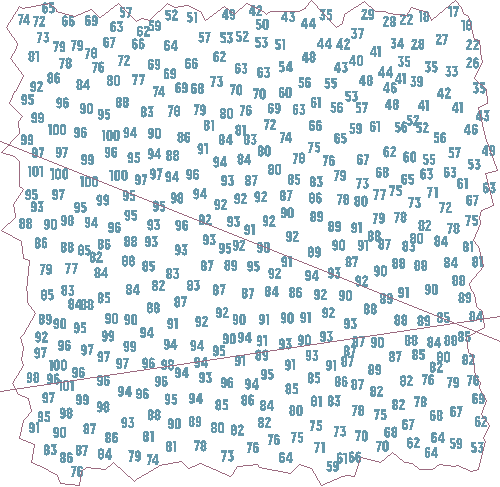
We've separated the high from the low! Now, just add water:
with headwater as (
select poly, height
from heightmap
join border on true
where height < 90
and not st_touches(poly, border.linestr)
order by random()
limit 30
)
select st_asewkt(st_centroid(poly)), height
from headwater;Alternatively, we could favor a more uniform distribution (central Squaria looks a bit desolate, and there's a river in the south flowing between four springs in a row); this spaces headwaters out much more effectively, but placement is the easy part and the current incarnation of Squaria illustrates an important point later on.
with headwater as (
select poly, height
from heightmap
join border on true
join (
-- draw a grid of horizontal and vertical lines 10 units apart
with x as (
select st_makeline(st_point(0, generate_series), st_point(100, generate_series)) as geom
from generate_series(10, 90, 10)
), y as (
select st_makeline(st_point(generate_series, 0), st_point(generate_series, 100)) as geom
from generate_series(10, 90, 10)
)
-- collect the points at which the horizontal and vertical lines cross
select st_collect(st_intersection(x.geom, y.geom)) as geom
from x
cross join y
) as grid on true
where height < 90
and not st_touches(poly, border.linestr)
and st_intersects(poly, grid.geom) -- pick polys at those intersection points
order by random()
limit 30
)
select st_asewkt(st_centroid(poly)), height
from headwater;And let it flow:
with river_poly as (
select
row_number() over () as id,
1 as iter,
1 as length,
headwater.poly,
headwater.height,
array[headwater.poly]::geometry[] as polys,
array[st_centroid(headwater.poly)]::geometry[] as centroids,
0 as lake_poly_depth
from headwater
union
select
-- neighbor_poly is null: we could not find a lower polygon to move into, sit here and lake up
previous.id,
previous.iter + 1 as iter,
case when neighbor.poly is null then previous.length else previous.length + 1 end as length,
coalesce(neighbor.poly, previous.poly) as poly,
coalesce(neighbor.height, previous.height + 2) as height, -- fill in lakebed
case
when neighbor.poly is null then previous.polys
else array_cat(previous.polys, array[neighbor.poly])
end as polys,
case
when neighbor.poly is null then previous.centroids
else array_cat(previous.centroids, array[st_centroid(neighbor.poly)])
end as centroids,
case
when neighbor.poly is null then previous.lake_poly_depth + 1
else 0
end as lake_poly_depth
from river_poly as previous
left outer join lateral (
select *
from heightmap
where st_touches(heightmap.poly, previous.poly)
and heightmap.height < previous.height
-- can't return to a poly with the same bounding box as a previously visited one
and not(heightmap.poly ~= any(previous.polys))
-- pick the closest centroid
order by st_centroid(heightmap.poly) <-> st_centroid(previous.poly)
limit 1
) as neighbor on true
-- border is a single-row relation so we can do this weird shortcut antijoin
inner join border on not st_touches(previous.poly, border.linestr)
where previous.lake_poly_depth < 5
)
select id, st_asewkt(st_makeline(centroids))
from river_poly
inner join (
select id, max(iter) as iter
from river_poly
group by id
) as maxiter
on maxiter.id = river_poly.id
and maxiter.iter = river_poly.iter;Alright, that one's a lot to deal with all at once. This recursive CTE is the very beating heart of our river generator. Like all recursive CTEs, it has a base term -- projecting a bunch of fields and initial values from headwater -- and a recursive term which works.... not quite how you might expect recursion to operate.
In Postgres, "recursion" is actually iteration. The base term is evaluated first, and its results placed in a "working table". Then, the recursive term is evaluated, with the self-reference river_poly indicating the working table. The results of the recursive evaluation become the new working table; if at this point there's anything in that working table, the recursive term is evaluated again.
The output of the CTE includes everything that has ever been in the working table. This is why the demo select has a self-join: to include only the final results for each river, rather than every step of each one's progress from headwater to cell to cell.
How does that progress happen, though?
The first thing you might notice is the projection logic that depends on whether neighbor.poly is null. Let's talk about neighbor first, though, in that lateral join below. Lateral join: the subquery is evaluated for each record, here from the working table (previous). So for each headwater in the first recursive execution, or for the last chunk of each river added in each successive iteration, we inspect neighboring polygons in the heightmap. We're looking for a lower polygon, not the lowest to avoid racing too quickly to local minima, and one which we haven't seen before for this river. Picking the closest lower centroid keeps things reasonably random and avoids some occasional funny-looking leaps across the landscape.
But wait. If we always move into lower neighboring cells, why do we need an additional check against retracing our steps?
The answer is local minima again. Our best efforts notwithstanding, it's easy for a river to flow into a cell surrounded by higher neighbors on all sides. Endorheic basins without outlets exist, but they're not that common (and lakes in them tend to be saline). So if a river enters such a basin, we want to give it a chance or several to exit again. We do this by simulating accumulation in a lake which raises the effective height of the current cell. On the next iteration, neighbors that were previously higher could be lower -- including that from which the river entered the lake cell, which is also by definition the closest lower centroid.
The neighbor.poly null checks in the select clause drive lake formation. When there's no valid neighbor, the river-in-progress increments its lake or effective height and stays still; otherwise, it proceeds into the neighboring cell, accumulating the neighbor's polygon and precalculating its centroid for later. Rivers get five chances to proceed at each iteration before they're excluded from the working table and terminate in an endorheic lake. At +2 per increment, this allows lakes to overcome a difference of up to 8 elevation points.
The last thing river_poly does is detect whether the river has reached the edge of the continent. The "weird shortcut antijoin" keeps rivers in the working table only as long as the last cell it moved into wasn't on the border.
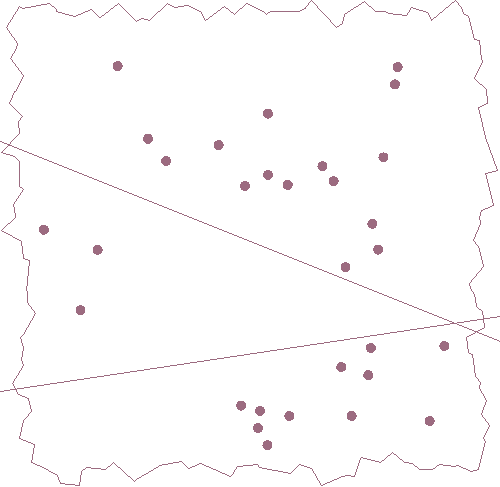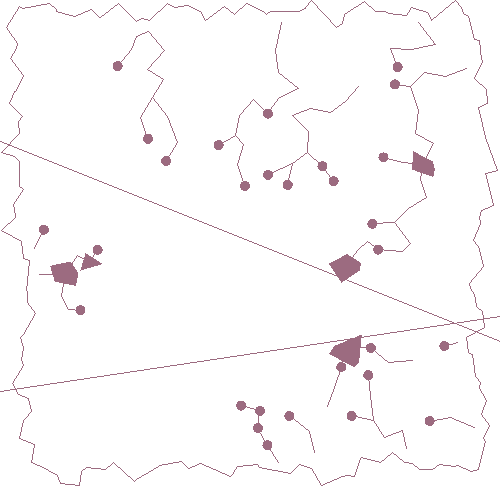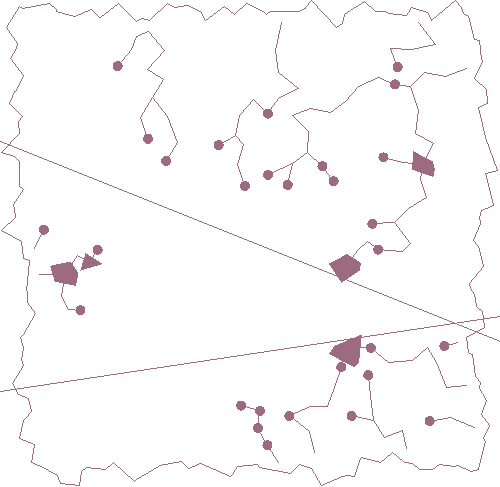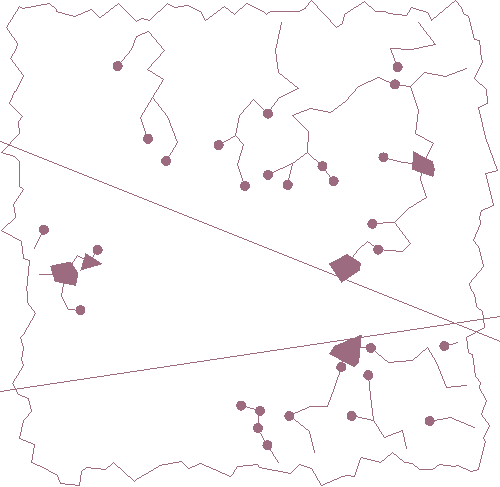
The "finished" flow hasn't quite reached the border because the rivers are drawn centroid to centroid, but making that connection is an st_closestpoint away.
That worked nicely! There's got to be a catch.
There are a few catches.
First, a philosophical question: after a river joins another, how many rivers do you have? You might be able to make a case for two at the confluence of the Rio Negro and Solimões, but that's an exception. If we mean this map to be useful, we can't be having two rivers occupy the same space all the way to the sea. One has to end and the other has to keep going.
Second, the output of the recursion includes as many records per river as the river has cells, because the working table is pushed into the result set for each cycle. We need to remove all non-final records.
Third: using lake formation to increase effective height and allow rivers to proceed enables a very specific paradox. A river alpha can flow into beta, but beta could there or further downstream enter and exit a lake, thereby increasing its effective height, and flow back into alpha. Simplified:
alpha flows east 51>---50>---------49>-------48
\ \
51-----<[46+6=52]-----<47-----<50 beta flows westYou can see this happening in the lower right of the gif, where two rivers start near each other just below the lower mountain range and meet in a lake -- actually, the triangular lake is filled first by the westward-flowing river, but is naturally downhill from the eastward-flowing river. On the next cycle, neither can exit, so the lake fills to depth 4 for westward and eastward forms its own
We already have the maximum iter for each river id, and checking for cross-confluence is a matter of looking for common centroids in differing orders:
with river_pruned as (
-- remove intermediary rows generated as river_poly recurses
select river_poly.*
from river_poly
inner join (
select id, max(iter) as iter
from river_poly
group by id
) as maxiter
on maxiter.id = river_poly.id
and maxiter.iter = river_poly.iter
where not exists (
-- if two rivers cross each other in opposite directions, pick the one with the lower
-- id and eliminate the other
select 1
from river_poly as rp2
where rp2.id < river_poly.id
and array(select * from unnest(rp2.centroids) where unnest = any(river_poly.centroids)) <>
array(select * from unnest(river_poly.centroids) where unnest = any(rp2.centroids))
)
)
select id, st_asewkt(st_collect(centroids)) from river_pruned;Pruning takes care of 2 and 3, but if you run this you'll see the same centroids appear several times in each river. We still need to ensure that a tributary is just a tributary and not the rest of the other river downstream from its confluence.
with cutoff as (
-- find the first point at which a river "loses" a confluence and becomes
-- subsumed in another river's flux
select
p.id,
min(array_position(p.centroids, confluence.centroid)) as position
from river_pruned as p
join (
-- centroids of all cells entered by more than one river; furthest upstream
-- wins, with lower ids breaking ties
select
unnest as centroid,
(array_agg(id::text order by ordinality, id))[1] as winner
from river_pruned
join lateral unnest(centroids) with ordinality on true
group by unnest
having count(*) > 1
) as confluence on confluence.winner <> p.id::text
and array_position(p.centroids, confluence.centroid) > 0
group by p.id
), river_line as (
select
river_pruned.id,
river_pruned.length,
river_pruned.poly,
river_pruned.height,
cutoff.position as cutoff,
river_pruned.polys[1:coalesce(cutoff.position, river_pruned.length)] as polys,
st_makeline(
case
-- only rivers which are not cut off and which come adjacent to the border
-- require the additional segment connecting to the shore!
when cutoff.position is null
and st_touches(
river_pruned.polys[coalesce(cutoff.position, river_pruned.length)],
border.linestr
)
then array_cat(
river_pruned.centroids[1:coalesce(cutoff.position, river_pruned.length)],
array[st_closestpoint(
border.linestr,
st_centroid(river_pruned.polys[coalesce(cutoff.position, river_pruned.length)])
)]
)
else river_pruned.centroids[1:coalesce(cutoff.position, river_pruned.length)]
end
) as geom
from river_pruned
left outer join cutoff on cutoff.id = river_pruned.id
join border on true
)
select id, length, cutoff, st_asewkt(geom)
from river_line;An aside: it took me a while to come up with the nearest-lower-neighbor approach, for no good reason. Before I got there, I still wanted to avoid a race to local minima, but did it with a truly random choice of lower neighbor for each river. Rivers crossed each other willy-nilly towards the sea, which I thought I'd address in a postprocessing step. This got absolutely cursed, involving another recursive CTE running window functions over unnested centroid arrays to eliminate confluence losers from all future contests. It's much, much better this way.
Anyway, at this point we're basically done! All that's left is to accumulate all the geometries for storage or display. Here's the final script:
fluviate.sql
with recursive envelope as (
select st_makeenvelope(0, 0, 100, 100) as geom
), voronoi_unclipped as (
select (st_dump(st_voronoipolygons(
g1 => st_generatepoints(
envelope.geom,
500 -- increase this for a finer polygon mesh
),
tolerance => 0.0,
extend_to => envelope.geom
))).geom as poly
from envelope
), voronoi as (
-- clip the Voronoi diagram to only those polys fully inside the envelope
select voronoi_unclipped.poly
from envelope
join voronoi_unclipped on st_contains(envelope.geom, voronoi_unclipped.poly)
), border as (
select st_boundary(st_concavehull(st_union(poly), 0)) as linestr
from voronoi
), mountain_range as (
with nonrandom_line as (
select st_makeline(st_point(0, v.y1), st_point(100, v.y2)) as linestr
from (values (70, 30), (20, 35)) as v (y1, y2)
)
select
st_collect(voronoi.poly) as geom,
st_collect(nonrandom_line.linestr) as linestr
from voronoi
cross join nonrandom_line
where st_intersects(voronoi.poly, nonrandom_line.linestr)
), heightmap as (
select
voronoi.poly,
-- height is a function of distance from the mountains, also factoring in
-- x-position (Squaria's east is lower than its west) and a little random
-- variance to make things interesting
100
- (min(st_distance(voronoi.poly, mountain_range.geom)) * 1.5)
- (st_x(st_centroid(voronoi.poly)) * 1.5 / 10)
+ (random() * 6 - 3)
as height
from voronoi
cross join mountain_range
group by voronoi.poly
), headwater as (
select poly, height
from heightmap
join border on true
join (
-- draw a grid of horizontal and vertical lines 10 units apart
with x as (
select st_makeline(st_point(0, generate_series), st_point(100, generate_series)) as geom
from generate_series(10, 90, 10)
), y as (
select st_makeline(st_point(generate_series, 0), st_point(generate_series, 100)) as geom
from generate_series(10, 90, 10)
)
-- collect the points at which the horizontal and vertical lines cross
select st_collect(st_intersection(x.geom, y.geom)) as geom
from x
cross join y
) as grid on true
where height < 90
and not st_touches(poly, border.linestr)
and st_intersects(poly, grid.geom) -- pick polys at those intersection points
order by random()
limit 30
), river_poly as (
select
row_number() over () as id,
1 as iter,
1 as length,
headwater.poly,
headwater.height,
array[headwater.poly]::geometry[] as polys,
array[st_centroid(headwater.poly)]::geometry[] as centroids,
0 as lake_poly_depth
from headwater
union
select
-- neighbor_poly is null: we could not find a lower polygon to move into, sit here and lake up
previous.id,
previous.iter + 1 as iter,
case when neighbor.poly is null then previous.length else previous.length + 1 end as length,
coalesce(neighbor.poly, previous.poly) as poly,
coalesce(neighbor.height, previous.height + 2) as height, -- fill in lakebed
case
when neighbor.poly is null then previous.polys
else array_cat(previous.polys, array[neighbor.poly])
end as polys,
case
when neighbor.poly is null then previous.centroids
else array_cat(previous.centroids, array[st_centroid(neighbor.poly)])
end as centroids,
case
when neighbor.poly is null then previous.lake_poly_depth + 1
else 0
end as lake_poly_depth
from river_poly as previous
left outer join lateral (
select *
from heightmap
where st_touches(heightmap.poly, previous.poly)
and heightmap.height < previous.height
-- can't return to a poly with the same bounding box as a previously visited one
and not(heightmap.poly ~= any(previous.polys))
-- pick the closest lower centroid
order by st_centroid(heightmap.poly) <-> st_centroid(previous.poly)
limit 1
) as neighbor on true
-- border is a single-row relation so we can do this weird shortcut antijoin
inner join border on not st_touches(previous.poly, border.linestr)
where previous.lake_poly_depth < 5
), river_pruned as (
-- remove intermediary rows generated as river_poly recurses
select river_poly.*
from river_poly
inner join (
select id, max(iter) as iter
from river_poly
group by id
) as maxiter
on maxiter.id = river_poly.id
and maxiter.iter = river_poly.iter
where not exists (
-- if two rivers cross each other in opposite directions, pick the one with the lower
-- id and eliminate the other
select 1
from river_poly as rp2
where rp2.id < river_poly.id
and array(select * from unnest(rp2.centroids) where unnest = any(river_poly.centroids)) <>
array(select * from unnest(river_poly.centroids) where unnest = any(rp2.centroids))
)
), cutoff as (
-- find the first point at which a river "loses" a confluence and becomes
-- subsumed in another river's flux
select p.id, min(array_position(p.centroids, confluence.centroid)) as position
from river_pruned as p
join (
-- centroids of all cells entered by more than one river; furthest upstream
-- wins, with lower ids breaking ties
select unnest as centroid, (array_agg(id::text order by ordinality, id))[1] as winner
from river_pruned
join lateral unnest(centroids) with ordinality on true
group by unnest
having count(*) > 1
) as confluence
on confluence.winner <> p.id::text
and array_position(p.centroids, confluence.centroid) > 0
group by p.id
), river_line as (
select
river_pruned.id,
river_pruned.length,
river_pruned.poly,
river_pruned.height,
river_pruned.polys[1:coalesce(cutoff.position, river_pruned.length)] as polys,
st_makeline(
case
-- only rivers which are not cut off and which come adjacent to the border
-- require the additional segment connecting to the shore!
when cutoff.position is null
and st_touches(
river_pruned.polys[coalesce(cutoff.position, river_pruned.length)],
border.linestr
)
then array_cat(
river_pruned.centroids[1:coalesce(cutoff.position, river_pruned.length)],
array[st_closestpoint(
border.linestr,
st_centroid(river_pruned.polys[coalesce(cutoff.position, river_pruned.length)])
)]
)
else river_pruned.centroids[1:coalesce(cutoff.position, river_pruned.length)]
end
) as geom
from river_pruned
left outer join cutoff on cutoff.id = river_pruned.id
join border on true
)
select
id,
st_collect(geom, points) as geom_with_points,
st_collect(geom, points) as geom_heightmap
from (
select
id,
st_collect(st_buffer(st_lineinterpolatepoint(geom, 0.0), 1)) as points,
st_collect(geom) as geom,
st_collect(poly) as polys
from river_line
group by id
) as river
union
select null, st_collect(poly, st_centroid(poly)), st_collect(poly, st_centroid(poly))
from (
select distinct poly
from river_poly
where lake_poly_depth > 0
and poly in (select unnest from river_pruned join lateral unnest(polys) on true)
) as lake
union
select null, linestr, linestr
from mountain_range
union
select
null,
st_collect(b.linestr),
st_collect(
st_translate(
st_scale(st_letters(round(h.height)::text), .03, .03),
st_x(st_centroid(h.poly)),
st_y(st_centroid(h.poly))
)
)
from heightmap as h
join border as b on true;